Replace Python Lists and Make Your Code Orders of Magnitude Faster!

No fancy libraries and no complicated engineering, just one data structure - hash tables.
Every beginner programmer loves for-loops because of their utility and how easy they are to understand. Similarly, everyone loves arrays. However more often than not, we start using arrays for everything without giving it a second thought. We take classes on data structures but when it comes to practicing what has been learnt, we fall short. It was only until recently that I caught myself falling into this trap. I was working with a programming task trying to challenge myself to write efficient and fast code.
We can do better!
In this post we will look briefly at dictionaries and sets in Python. We will (re)discover the power of these data structures in making data operations super fast in our code. We will learn how hash tables can lead to huge algorithmic performance improvements.
But first we need to review some concepts.
Time to go back to basics!
Back to basics: Hash tables
Data structures in programming languages are implementations of abstract data structures in Computer Science. Python dictionaries and sets are basically a hash table. A hash table is an implementation of an abstract data structure called an associative array, a dictionary or a map. In simple terms, a hash table is a mapping from keys to values. Given a key, the data structure can be queried to get the corresponding value.
A simple way to implement this would be a direct address table or an array.
So for a key 1 we would store the value in index location 1 of the array.
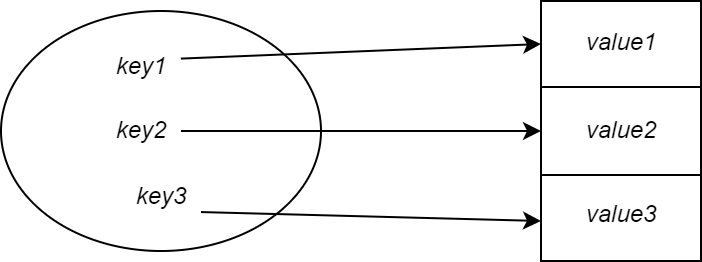
Each key simply maps to the next slot in the array.
There is one problem with this approach though. If there are a lot of keys, the size of the array would be huge. This would make it infeasible to store memory-wise.
A solution to this is to use a hash function. A hash function is responsible for mapping a key to a value stored in a hash table. You pass it a key and it spits out a value called a hash value. The hash value determines where in the hash table to store the value corresponding to the key. In other words it is an index.
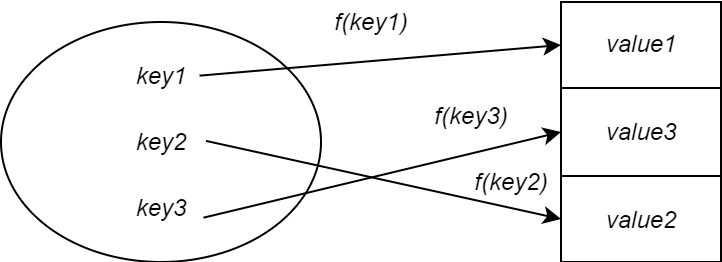
Now, the size of the hash table would be smaller than the size of the direct address table. This means a hash table is feasible to implement memory-wise. However, this also means that two keys can map to the same value. This is called a hash collision and occurs when the hash function outputs the same value given two distinct keys.
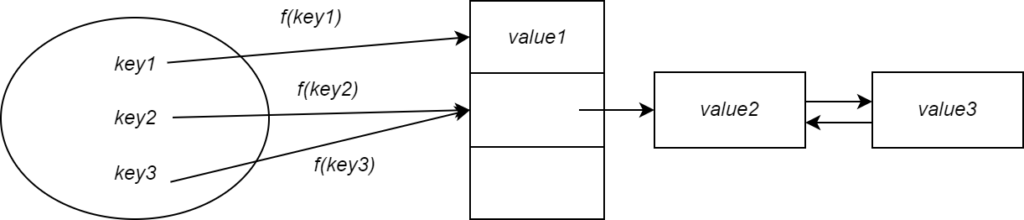
To resolve this, we can store the values in a linked list if two keys hash to the same value. Any subsequent collision would simply cause the value to be appended to the linked list. This is called collision resolution by chaining.
Now you can imagine if all keys get hashed to the same value they would all be added to the linked list meaning the performance would be no better than using a list!
Hash tables are resized if they get too full. The threshold is called the load factor and determines the ratio of occupied slots to available slots. Usually when the value is over 3/4 the hash table gets resized. This ensures that the linked lists never get too full and ensures the promised average case performance. Finally, hash functions are usually chosen in such a way that they distribute keys uniformly across the slots. This means the chance of a collision is very small to begin with.
Great! Now let’s look at some big O notation.
Back to basics: O(1) vs. O(n)
Searching for elements in an array has an average case time complexity of O(n) since we need to traverse the list linearly to find the element. The larger the size of the list, the longer it would take to search for an element. You can visualize this as a line of people standing and where you start from the leftmost person and ask if he is the one you are looking for. If not you ask the person next to him and so on. You can imagine it would take longer to find the person if there are a 1000 people vs 10.
For a hash table though, the average case time complexity for a search is O(1) – it is constant. No matter the size of the number of elements you store whether that is a million or 10, it would always take a constant unit of time to find an element. In other words it would be fast for all sizes of input. You can imagine a group of people standing and one extra person who is your helper. To find the person you simply ask the helper instead of searching through the group. The helper tells you instantly where your person of interest is.
Insertion and deletion of elements is also O(1).
Click here for a really nice cheat sheet for data structures and big O.
Alright, time to code now and see hash tables in action!
Code & benchmarks
We are going to simulate the following task:
- A list
Lthat contains elements from 0 to 100,000 in sorted order. The third last index has a randomly generated negative value in the range from 0 to 100,000. - A list
Rthat contains elements from 0 to 100,000 in sorted order.
The task is simple. We need to find the value in L that does not appear in R.
I know there are simpler ways to solve this problem but for the purposes of learning we will attempt a more elaborate approach.
The solution function is a naive implementation of a solution. We iterate over L and for each element check whether it exists in list R. The in operator checks membership and is akin to doing a search operation.
If it exists we simply return the negative integer.
The elapsed time for this solution is approximately 60s.
If we analyze the code for the solution function we see that the time complexity is O(n2).
This is because for each element in L we are traversing R and checking for membership. The for loop takes O(n) as it runs for n steps. For each step we do O(n) operations as we need to check every element in list R and see whether its the one we are looking for.
This gives O(n)*O(n)=O(n2)
The operation runs in quadratic time. The time it takes would be equivalent to the square of the input size. You can imagine how taking the square of larger and larger numbers yields ever-increasing larger values.
What can we do to improve this?
Instead of traversing R to check for membership we can implement R as a hash table instead of an array. Time complexity for checking for membership would therefore be O(1).
As a result, the operation would take O(n)*O(1)=O(n).
This is linear in the size of the input! So the time it takes would be proportional to the input size (as opposed to quadratic).
Wait till you see the performance improvements!
Timing solution2 gives an elapsed time of 0.011s. This is an improvement of over 5000x !
Conclusion & closing remarks
In summary, you have learnt the motivation behind using hash functions and hash tables.
We have looked briefly at big O notation for hash tables and compared it with that of arrays.
To top it all off, we have looked at an implementation that makes use of hash tables to solve an algorithmic problem in record time.
As software engineers we must know the right tool to use for the right situation and not try to brute-force techniques in every scenario we come across.
With that in mind, there are a few points to remember.
Like all things hash tables are not a silver bullet. They will not fit every use case. For instance, duplicate elements cannot be stored in hash tables. So if your use case requires that, you are better off using an array. Similarly, hash tables are not sorted. If your use case requires a sorted data structure, hash tables are not the answer. Lastly, there are no built-in functions to find the maximum or minimum elements in a hash table. Finally, the time complexities mentioned above are average case. There can be situations where a worst case occurs meaning hash tables would perform the same as arrays.
I hope you enjoyed the content of this post. Until next time.
You can see more code articles here.
Resources
Cormen Thomas H et al, Introduction to Algorithms (MIT Press, 2009).
